If properly architected, there’s now a world of applications in which AI enables 5G, and a world where 5G enables AI, all collapsed in a transparent manner for enterprise, telco, and the edge.

5G brings wireless convenience combined with the speed and reliability of wired connections as where AI brings unprecedented intelligence to machines through training, heuristics, and inference. Intelligent machines let us achieve a new dimension of efficiency and reliability to automation. Think of a fully autonomous car needing to apply brakes, without human involvement, in a matter of milliseconds. Then, imagine a robot on a factory floor with micrometers of precision.

Traditionally, communications (5G) and compute (AI) are treated as two mutually exclusive topics. At the application level, 5G and AI complement each other. There can be AI-enabled by 5G as well as 5G enabled by AI. When it comes to basic operations and hardware requirements, these two fields are not mutually exclusive.

Synergies between AI and 5G
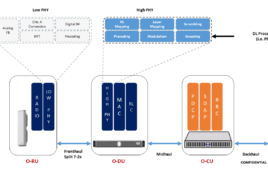
There are some basic functions in wireless communication, like: time to frequency and frequency to time conversion, popularly known as Fast Fourier Transforms (FFT) and inverse Fast Fourier transforms (iFFTs), modulation, demodulation, channel estimation, equalization, and MIMO detection, and more (Figure 1). It turns out that the mathematics for these functions are comprised of operations such as:

• Dot-product multiplication for FFT and channel estimation
• Equalization
• MIMO/user detection, which indicates max and average of a vector, etc.

The basic functions of AI include convolution, pooling (average and max), nonlinear functions (like ReLU), normalization, and more. It turns out, the math behind many of these functions is also comprised of very similar mathematical operations found in 5G. From an implementation perspective, these two fields are not mutually exclusive. If you look at the literature, many machine learning concepts originated from information theory itself.

A closer look
The basic mathematical operation of dot-product multiplication is pervasive in 5G and communications in general. Dot-product multiplication is required to compute FFT, channel estimation, and many other operations in communications. This operation is typically done over 16-bit complex numbers. Convolution is the most common mathematical function used in AI.

During this process, a weight matrix slides over the data matrix, and does dot-product multiplication, these are typically 8-bit, 16-bit, or 32-bit real numbers. You will immediately notice that the multiplier operation is common. The data feeds to the multipliers differently.

In communications, channel estimation extracts useful information from the ingress data. The transmitter inserts several pilot tones in the transmitter data. The receiver feeds the pilot tones to averaging hardware to estimate the channel. Weighted averaging, or normal averaging, is then used depending on the type of channel.

What is the mathematical corollary in AI? Average pooling is a common operation in the field of AI to reduce data size and to provide invariance to rotation, translation, and down sampling. An AI engine should identify a cat, irrespective of its orientation. After all, an upside-down cat is still a cat. Averaging provides invariance to this rotation. Notice how the same hardware is utilized to compute averaging of a given data set.

Look at another pooling example related to 5G: finding the maximum or a peak. To enable a call, the user must establish a handshake with the nearest base station. Determining the peak of incoming data is typically implied in communication to identify the users and their timing. The waveforms of different users feed to the max-pooling hardware. Once the peak occurs, the base station identifies the presence of a user and its timing. The user may now link to the base station.

Another direct application in telco, specifically open RAN, is during eCPRI compression and decompression. Max estimation is used to find maximum tone, and therefore bit occupancy corresponding to that tone. The communication systems field is full of many such examples. In the field of AI, max pooling is typically used to reduce the data size while keeping the translation invariance.

The same max-pooling hardware applies to AI. While we often treat 5G and AI as two distinct topics, both utilize the same computation hardware and mathematical operations. The same hardware for dot-product multiplication and convolution, as well as average and max pooling, are not only analogous, but both fields can harness it.

Another commonality between 5G and AI inference acceleration is their unforgiving, mission-critical nature. Every microsecond of latency matters and, in some cases, is the difference between life and death, profitability and loss. Thus, both rely on memory locality (Figure 2). For example, in 5G, receiving a phone call requires data to be processed within a fraction of a millisecond. Applications requiring ultra-reliable low latency communication (URLLC) need access to memory even faster. In both fields, time to memory access is crucial. Neither can afford to store or access memory off-chip. By no surprise, when we analyze both 5G and AI, the on-chip memory requirements are the same.

Let us apply the locality principle to examples of memory-bound operation. As discussed before, in the 5G physical layer, FFT is a very time-critical operation. The typical FFT over 4K data takes only a few hundred nanoseconds, making on-chip memory imperative. Similarly, the hybrid automatic repeat request (ARQ) process requires on-chip memory. For AI inferencing, such as level four driving, inferencing decisions need to be made in a matter of milliseconds. For data center AI, even millisecond delays in inferencing can cost billions of dollars in revenue.

Lastly, nonlinear functions are a common mathematical operation employed in 5G and AI. In 5G, 1/X is used to compute signal-to-noise ratio and normalize input data. The sqrt(X) is used to find the magnitude of a complex number. Consider Euler’s formula, which represents a complex number as sine and cosine. In communication, rotation of this phasor is of interest. Then we use the arctan operation to compute that rotation.

Common nonlinear activation functions in AI
For the starters in AI, neural networks are great universal function approximators. To be able to apply any function, we need nonlinearity. That’s where the activation functions come in. They add nonlinearity to neural networks. Without activation functions, a neural network can be considered just as a collection of lead-in models. Few of these activation functions are: Tanh-hyperbolic, Swish, Sigmoid, Softmax, ReLU, and others.

The same basic hardware that creates nonlinear functions for communication can create nonlinear activations for AI applications. For 5G and AI math enthusiasts, we do not create dedicated hardware for each of these functions. Instead, we perform piecewise nonlinear approximations, on a second order polynomial, based on Taylor’s series expansion. Once this approximation is created, any nonlinear function can be realized using the same hardware.

Conclusion
As academics, many of us are drawn to synthesizing correlation unseen by most. As technologists, we derive new unstated forms. The art in all of this is in the design. The discovery is that 5G is a natural support set of AI, where 5G requires extra processing elements, like Forward Error Correction (FEC), encoders/decoders, beamforming, and factor crossing, etc. An AI inference accelerator requires more emphasis on memory locality and host software.

Adil Kidwai is VP of Product Management at EdgeQ. He has over 18 years of leadership experience developing core wireless technologies such as 4G/5G, WiFi, WiMAX, and Bluetooth. As a lead architect and technologist at Intel, Adil drove pervasive adoption and market success of wireless communications into high growth client markets such as Phones and PCs. He was also the Director of Product and IP Architecture at Intel Communication Device Group where he was responsible for 4G/5G Modem architecture, IPs and power optimization. He then became the Director of Engineering in the field of Artificial Intelligence / Machine Learning, focusing on L4/L5 Autonomous Driving and Datacenter Inference. He holds a Bachelor of Technology in Electrical Engineering from Indian Institute of Technology, a MS from UCLA, and an MBA from UC Berkeley.