Magnitude and phase imbalance are important specifications to understand, when testing high-speed devices with differential inputs like analog-to-digital converters, amplifiers, mixers, and baluns (just to mention a few).
Great care must be given when implementing analog signal chain designs using 500 MHz frequencies and above, as all devices (active or passive) have some sort of inherent imbalance across frequency. Not that 500 MHz is, by any means, a magic frequency point. Based on experience, this is where most devices start to deviate in phase balance. Depending on the device, this frequency could be much lower or higher.
Let’s take a closer look in detail using this simple mathematical model below:
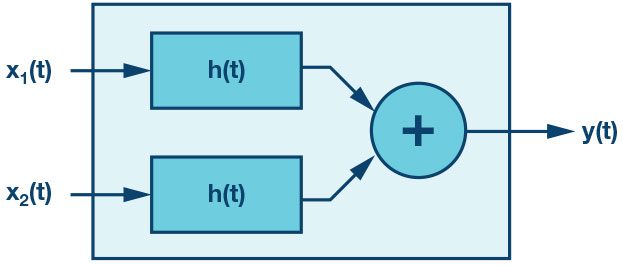
Figure 1. Mathematical model with two signal inputs.
Consider the inputs x(t) to an ADC, amplifier, balun, etc., or any device that converts signals from single-ended to differential, or vice versa. The pair of signals, x1(t) and x2(t), are sinusoidal and, therefore, the differential input signals are of the form below:
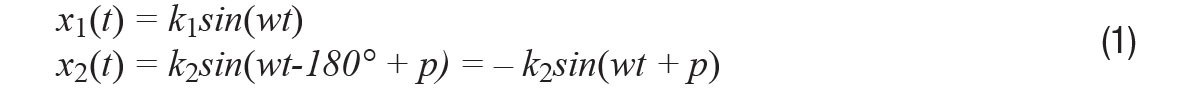
If not, even order distortion test results of the ADC can dramatically vary over the operating frequency range directly due to the amount of imbalance in these components.
The ADC, or any active device for that matter, can be simply modeled as a symmetrical third-order transfer function:
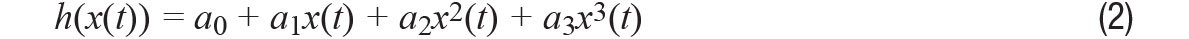
Then,
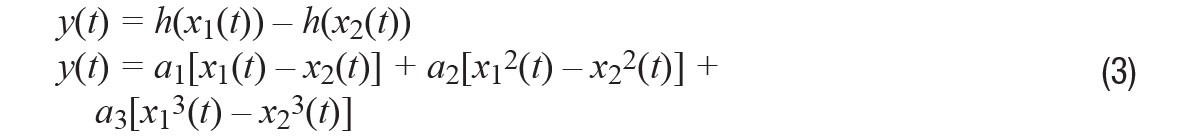
In the ideal case, where we have no imbalance, the transfer function of the simple system above can be modeled as follows:
When x1(t) and x2(t) are perfectly balanced, they have the same magnitude (k1= k2= k) and are exactly 180° out of phase (φ = 0°).

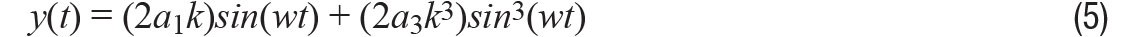
When applying the trigonometric identity for powers and gathering terms of like frequency we get:
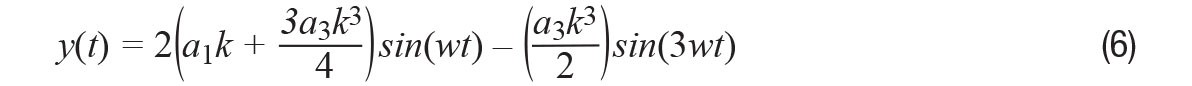
This is the familiar result for a differential circuit: even harmonics cancel for ideal signals, while odd harmonics do not.
Now suppose the two input signals have a magnitude imbalance, but no phase imbalance. In this case, k1≠ k2, and φ = 0.

When we substitute Equation 7 for Equation 3 and again apply the trigonometric power identities:
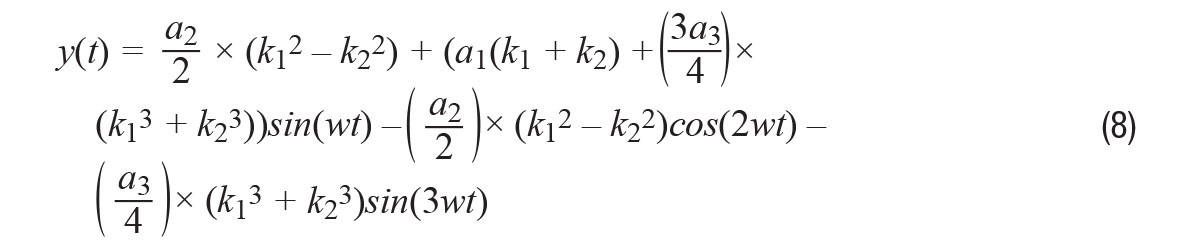
We can see from Equation 8 that the second harmonic is proportional to the difference of the squares of the magnitude terms k1 and k2, or simply put:

Now, let’s assume that the two input signals have a phase imbalance between them with no magnitude imbalance. Then, k1 = k2, and φ ≠ 0.

Substitute Equation 10 in Equation 3 and simplify:
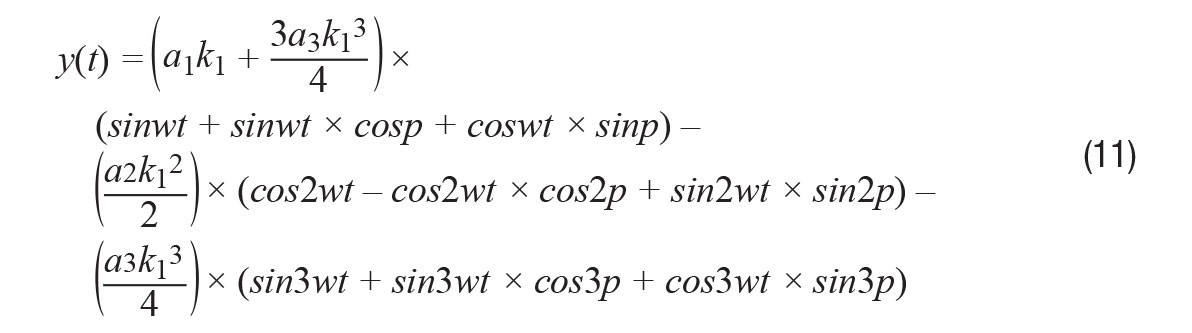
From Equation 11, we see that the second-harmonic amplitude is proportional to the square of the magnitude term, k.

If we go back and do a comparison of Equation 9 and Equation 12, and assume my trigonometry IDs are in good shape, it all boils down to this; the second harmonic is more severely affected by phase imbalance than magnitude imbalance. For phase imbalance, the second harmonic is proportional to the square of k1—again, look at Equation 12, while for magnitude imbalance, the second harmonic is proportional to the difference of the squares of k1 and k2, or Equation 9. Since k1 and k2 are approximately equal, this difference typically ends up being small—especially if you compare it to a number that is squared.
Testing HS Amplifiers
Let’s move onto a use case, as is shown in Figure 2. Here, we see a block diagram that shows a test setup for HD2 distortion testing typically used in the lab of a differential amplifier.

Figure 2. HS amplifier HD2 test setup.
At first glance, this seems pretty straightforward—however, the devil is in the details of this test. If we look at Figure 3, we see a battery of HD2 test results using all the same components in this block diagram, differential amplifier, baluns, attenuators, etc. What was completed in these tests was to show that the simple mismatch in phase, just by flipping the balun orientation in different ways, can produce different results across the HD2 frequency sweep. There are two baluns in this setup, so this can create four possible scenarios by reversing their connections on one or both sides of the setup. The results are shown in Figure 3.
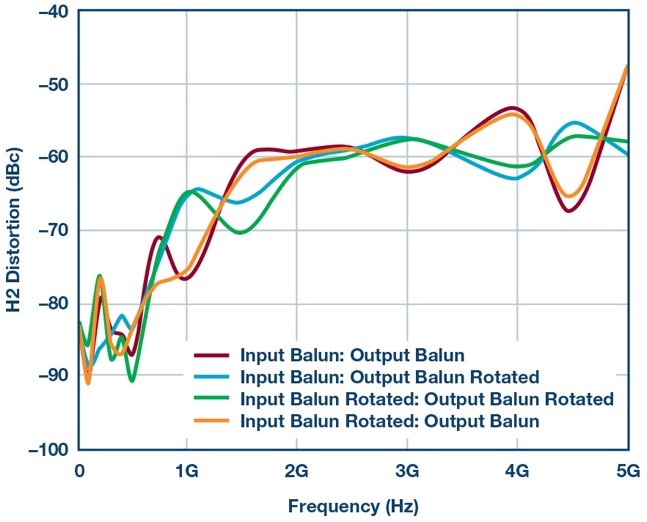
Figure 3. Testing HD2 performance with Vendor 1A balun using different balun orientations.
The amount of variance in HD2 distortion curves revealed in Figure 3 proves a further look at the balun’s performance is needed, specifically for phase and magnitude imbalance. The following two figures show the phase and magnitude imbalance of several baluns from various manufacturers. A network analyzer was used for the imbalance test measurements.
The red traces in Figures 4 and Figure 5 correspond to the actual balun used to acquire HD2 distortion data in Figure 3. This particular balun, from Vendor 1A, had one of the highest bandwidths and good pass-band flatness, but worse phase imbalance as compared to the other baluns over the same 10 GHz frequency test band.
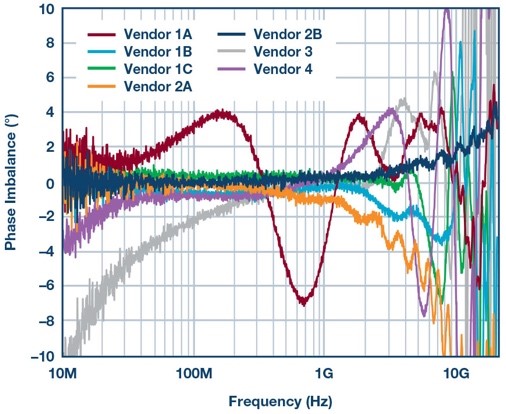
Figure 4. Phase imbalance of various baluns.
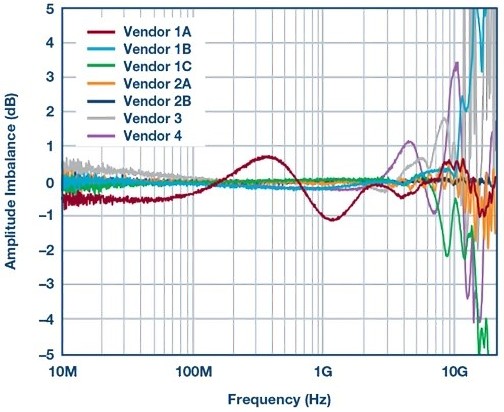
Figure 5. Magnitude imbalance of various baluns.
The next two figures represent a retest of HD2 distortion using the best balun that had the lowest phase imbalance found in Figure 6 and Figure 7, from Vendor 1B and Vendor 2B, respectively. Notice that with better imbalance performance, HD2 distortion variance is reduced accordingly, as seen in Figure 7.
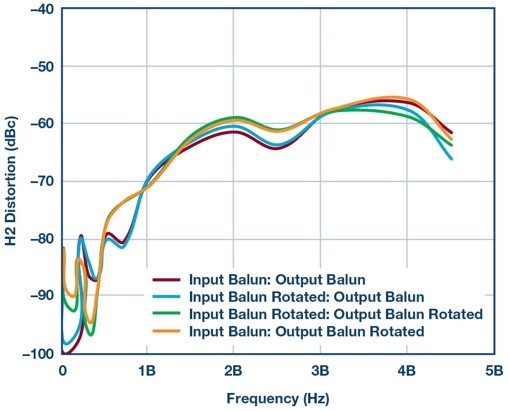
Figure 6. Retesting HD2 performance with Vendor 1B balun using different balun orientations.
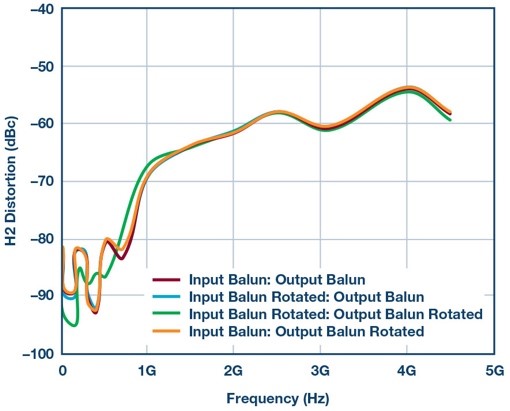
Figure 7. Retesting HD2 performance with Vendor 2B balun using different balun orientations.
To further illustrate how phase imbalances directly affects the performance of even order distortion, Figure 8 shows HD3 distortion over the same conditions as the previous HD2 figure. Notice how all four traces are roughly the same, as expected. Therefore, as proven in the mathematical derivation example shown previously, HD3 distortion is not as sensitive to imbalances in the signal chain.
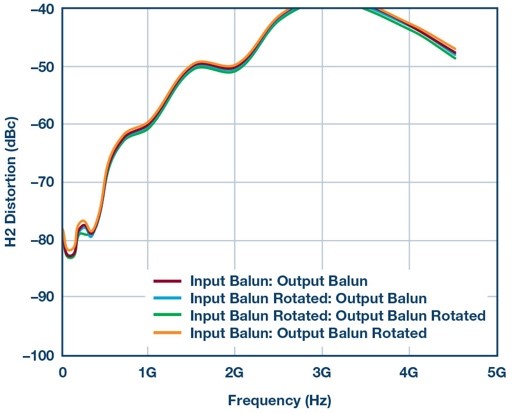
Figure 8. Testing HD3 performance with Vendor 2B balun using different balun orientations.
Until this point, it should be assumed the input and output-connected attenuator pads, as shown connected in Figure 2, are stationary and did not change during the balun orientation measurements. The next figure represents the same traces shown in Figure 7, testing only Vendor 2B’s balun performance as the attenuators are swapped between inputs and outputs. This generates another set of four traces, shown as dashed lines in Figure 9. The result is that we are back where we started, as this shows up as more variation in the test measurement. This further underscores that small amounts of mismatch in either side of a differential signal pair matters at high frequencies. Keep in mind to document your test conditions in detail.
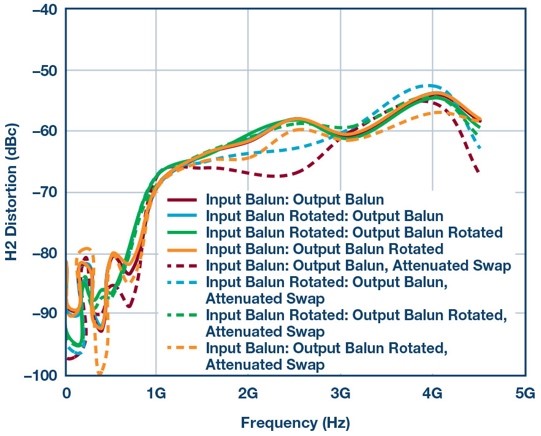
Figure 9. Testing HD2 performance with Vendor 2B balun only using different balun orientations and attenuation pad swaps.
Balancing It All Out
In summary, all things matter when developing fully differential signal chains in the GHz regions; that is, attenuators pads, baluns, cables, traces on a PC board, etc. We have proven this mathematically and in the lab using a high-speed differential amplifier as our test bed. So, before we start to blame the part or the vendor, please take extra special care during the PCB layout and lab testing.
Lastly, you might be asking yourself, so how much phase imbalance can I tolerate? When I pick up a balun, for example, and it says x-number of degrees of phase imbalance at x-GHz, what does that mean in terms of degradation to my part or system? Can I expect a certain amount of loss or degradation in dB’s of linearity performance?
This is a difficult question to answer. Ideally, if everything in your signal chain were matched perfectly, there would be no even order distortion to contend. Second, it would be nice to have a rule of thumb or equation that says for every x° of phase imbalance, one should expect x dBs of loss in linearity (HD2 degradation). However, this cannot be the case because every component (active or passive and differential in nature) has some sort of inherent phase mismatch. There is just no way to perfectly balance an IC design internally, or cut cables with absolute perfectly matched length. No matter how small these mismatches are, they become more pronounced as higher and higher frequencies are utilized in a system.